研究
研究の興味:情報科学と物質科学の融合による非平衡開放系の強相関物理の理論
- 凝縮系理論: 強相関量子(電子)系
- AMO(Atomic Molecular, and Optical) 物理: 冷却原子系、量子開放系、非エルミート系
- 量子多体物理・量子情報: 連続測定下のダイナミクス
キーワード
超伝導、フェルミ超流動、朝永ラッティンジャー液体、近藤効果、(遍歴)強磁性、SU()対称性、非平衡定常状態、観測誘起相転移、エンタングルメントエントロピー、量子測定、完全計数統計
手法
場の理論、共形場理論、ベーテ仮説法、密度行列繰り込み群(及びその非エルミート系への拡張)、動的平均場理論、(時間依存)一般化ギブスアンサンブル、量子トラジェクトリー法、量子測定理論
研究の詳細
量子開放系における超伝導(フェルミ超流動)
- 非エルミート超伝導の理論 Phys. Rev. Lett. 123, 123601 (2019) (Highly Cited Paper in Web of Science)
- 例外点と Van-Hove 特異点の効果 Phys. Rev. B 109, L060501 (2024)
- 散逸のある非対称ホッピングの系 Phys. Rev. B 110, 184518 (2024)
近年の冷却原子系の実験的発展に着想を得て、我々はフェルミオンの非弾性散乱がもたらす散逸によって生じる、複素相互作用を持つ非エルミート BCS ハミルトニアンの解析を行いました。我々は超伝導理論の基盤をなす BCS 理論を非エルミート系に世界で初めて拡張し、非エルミート系に特有の非従来型の相転移が起こることを発見しました。具体的には、強い散逸によって一度壊れた超伝導が復活し、これが非エルミート系特有の特異な物理現象を引き起こす例外点に由来するものであることを明らかにしました。
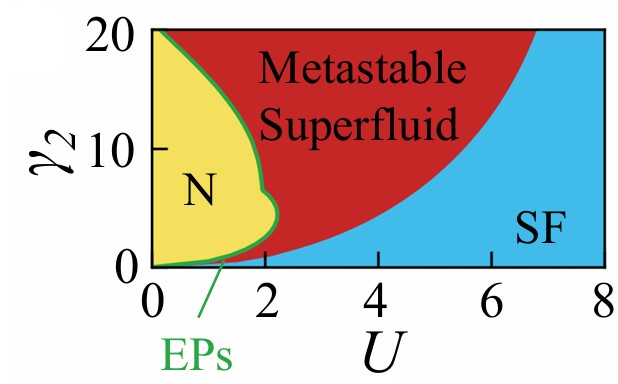
非エルミート超伝導の相図: 相互作用()と散逸()の依存性を超伝導ギャップ方程式から求めた図。常伝導相(N)と超伝導相(SF)の間に新たな超伝導相が出現している。
- スピン対破壊効果による例外点を伴う超伝導の出現 Phys. Rev. Lett. 135, 266002 (2025) プレスリリース
さらに我々は、スピン対破壊効果と呼ばれるスピンに依存した散逸のある非エルミート BCS 超伝導の解析を行い、従来とは全く異なる超伝導相を発見しました。これまでは例外点は相境界上にのみ現れると考えられてきましたが、この新しい相では、例外点が安定な超伝導と共に出現することを明らかにしました。さらに、エネルギーが複素の値を取る非エルミート系特有の性質を反映した状態密度を用いて、例外点を伴う超伝導が出現するメカニズムを解明しました。
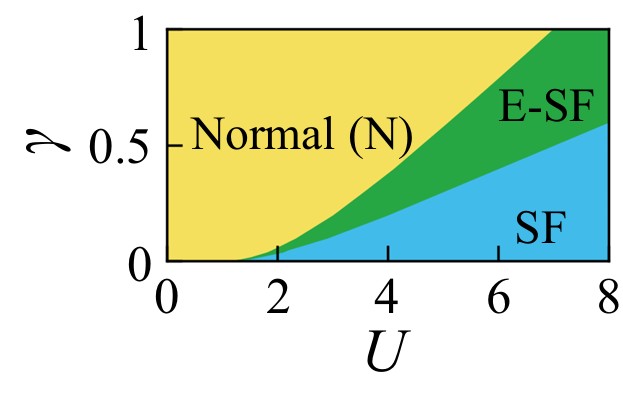
スピン対破壊効果のある非エルミート超伝導の相図。例外点を伴う新しい超伝導相(E-SF)が出現する
- 超伝導の動的相転移 Phys. Rev. Lett. 127, 055301 (2021) 我々は超伝導を形成するクーパ対の二体ロスがもたらす散逸によって引き起こされる、超伝導の集団励起と非平衡相転移の新しいメカニズムを理論的に予測しました。まず、我々は BCS 理論をリンドブラッド方程式で記述される量子開放系のダイナミクスに拡張しました。その結果、実験的に実現が期待される超伝導のジョセフソン接合系に散逸を導入すると、直流ジョセフソンカレントの消失によって特徴付けられる、非平衡動的相転移が引き起こされることを明らかにしました。
散逸下の朝永ラッティンジャー液体:
- 散逸下の朝永ラッティンジャー液体における普遍的性質 (Phys. Rev. B 105, 205125 (2022))
XXZ スピン鎖と呼ばれる典型的なスピン系における臨界現象は朝永ラッティンジャー (TL) 液体によって記述されることが知られています。我々は散逸の存在する非エルミート XXZ スピン鎖において、相関関数を求め有限サイズスケーリングを行うことによって、非エルミート臨界現象の普遍的性質を明らかにしました。この研究では強相関系における幅広い理論的手法を非エルミート系に拡張、及び適用しました(ボゾン化、共形場理論、ベーテ仮説法、非エルミート密度行列繰り込み群など)。これらの強力な系統的手法によるアプローチにより、非エルミート TL 液体は複素 TL パラメータによって特徴付けられる普遍性クラスに属しており、これが共形場理論の複素拡張で記述されることを明らかにしました。
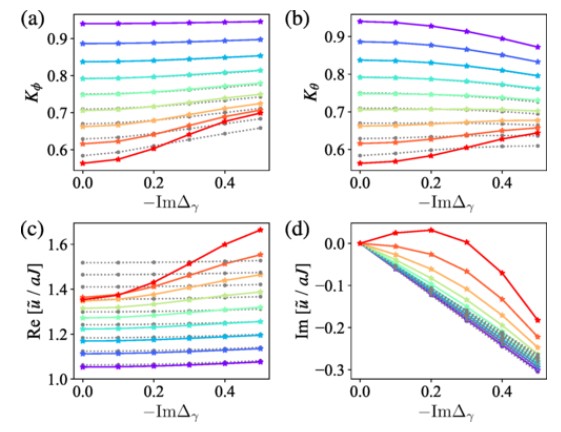
非エルミート密度行列繰り込み群とベーテ仮設法により得られた (a),(b) 臨界指数、(c),(d) 素励起の速度
- 散逸下の朝永ラッティンジャー液体における普遍的性質:対称性を持つ系への拡張 (Phys. Rev. B 107, 045110 (2023)) 近年冷却原子系において、ハバードモデルなどに代表される対称性を持つ量子系の実現が報告されました。例えば固体電子系はの二種類のスピンを内部自由度として持ちます。冷却原子系においては、これを種類の内部自由度に拡張したような系が、核スピンの自由度を用いることによって自然に実現されます。我々はこのような対称性が存在する一次元量子臨界系において、散逸によって誘起された普遍的性質をフェルミオン、及びボゾンの一般系に大して明らかにしました。その結果、スピン対称性を持つ散逸下の TL 液体は、 ガウシアン共形場理論の複素拡張によって記述されるチャージモードと、level- Kac-Moody 代数によって記述される個のスピンモードの和で特徴づけられることを明らかにしました。その結果、臨界指数などはチャージの指数しか散逸の影響を受けず、これが非エルミート系へのスピンチャージセパレーションの拡張となっていることを明らかにしました。
量子測定下のダイナミクスにおける相転移と普遍性:
-
量子多体局在系における観測誘起相転移 (Phys. Rev. B 107, L220201 (2023))
-
量子多体系における部分系揺らぎの観測誘起クロスオーバとポストセレクションの回避 (arXiv:2503.02418)
近年、量子情報や AMO 物理、統計物理などの幅広い分野において、観測の反作用によって誘起されたダイナミクスの研究が盛んに行われており、観測誘起エンタングルメント相転移などの新奇な相転移が報告されています。我々は、観測の反作用と乱れが共存する物理系を考え、観測誘起相転移と、それに伴うエンタングルメント相図を得ました(図 a)。さらに、フィデリティと呼ばれる物理量の解析により、観測の反作用と乱れによる局在はそれぞれダイナミカルに異なる性質を持つことを明らかにしました。また、一般にはこのような系を実現するのは、ポストセレクションと呼ばれる問題により困難であることが知られていますが、我々はこれを回避する一般的な手法を冷却原子系において提案しました。さらに、量子スピン系で測定結果の揺らぎのダイナミクスを理論的に追いかけることで、全系のダイナミクスは自明であるにもかかわらず、内部系の揺らぎには、測定に誘起された非自明な多体効果が現れることを明らかにしました(図 b)。また、これが典型的な量子多体スピン模型においてパラメータによらず現れることを示し、新たな普遍性の存在を示唆する結果を得ました。特に、測定結果の揺らぎはポストセレクションが不要であり、実験的に極めて低コストで実現可能なことも示しました。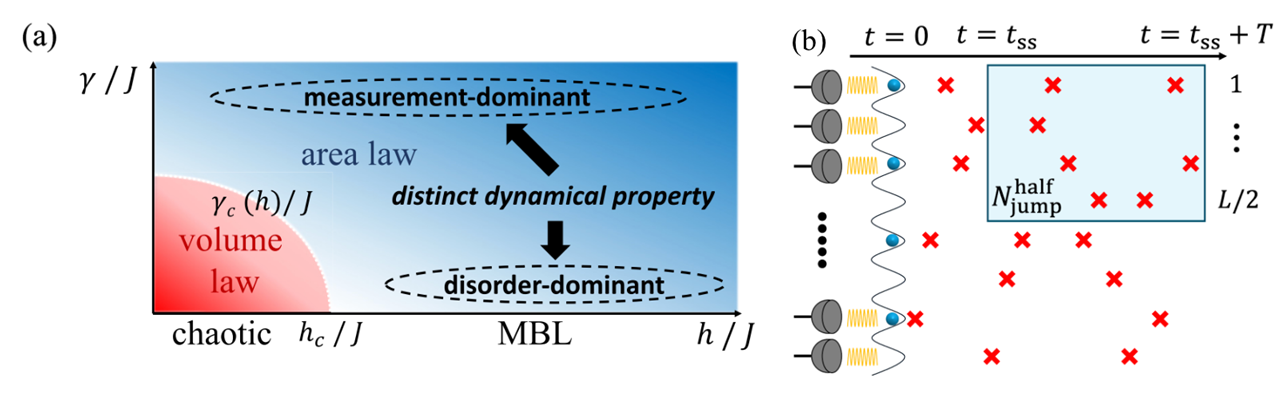
(a): 観測と乱れが共存する環境下でのエンタングルメント相図 (b): 量子測定下のダイナミクスと内部系での揺らぎ
-
準周期系における観測誘起相転移 (Phys. Rev. B 112, 054309 (2025)) 近年、周期性はないものの、規則的な配列を示す準周期系と呼ばれる物理系が注目を集めています。例えば1次元系ではフィボナッチ数列、2次元系ではペンローズタイル等が知られています。我々は定常状態のエンタングルメントエントロピーを準周期系で数値的に解析し、観測と準周期性の競合で観測誘起相転移が起こることを理論的に明らかにしました。

ペンローズタイル
非平衡定常状態:
- 散逸に誘起された非相反輸送 (Phys. Rev. Research 2, 043343 (2020))
整流現象(ダイオードなどの一方向性の流れを伴う現象)に代表される非相反現象は、凝縮系物理や非平衡統計物理など幅広い分野で長らく注目を集めてきました。我々は、非平衡定常状態において、一方向に粒子が流れる minimal な模型を提案しました。具体的には、非平衡状態にある熱浴と平衡状態にある熱浴が結合した 1 次元フェルミ粒子系を考えました。まず、散逸が非相反である場合に、どのような条件で整流が生じうるのかを導出しました。さらに、散逸が相反であっても、空間反転対称性と時間反転対称性の両方が破れていれば、整流が生じうることを明らかにしました。
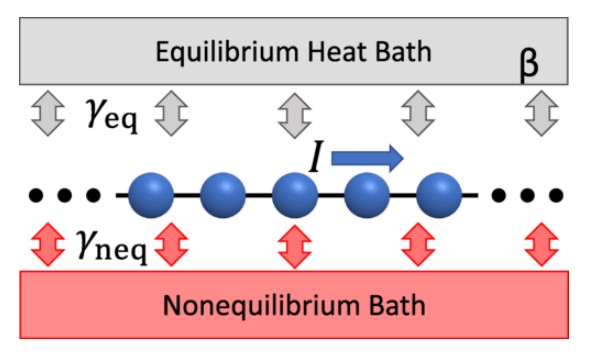
熱浴との結合によって整流が生じる図